Зеркальная антенна
Зеркальная антенна
Общие сведения и принцип действия
зеркальной антенны.
Зеркальными
антеннами называют антенны, у которых поле в раскрыве формируется в результате
отражения электромагнитной волны от металлической поверхности специального
рефлектора (зеркала). Источником электромагнитной волны обычно служит
какая-нибудь небольшая элементарная антенна, называемая в этом случае
облучателем зеркала или просто облучателем. Зеркало и облучатель являются основными
элементами зеркальной антенны.
Зеркало
обычно изготовляется из алюминиевых сплавов. Иногда для уменьшения парусности
зеркало делается не сплошным, а решетчатым. Поверхности зеркала придается
форма, обеспечивающая формирование нужной диаграммы направленности. Наиболее распространенными
являются зеркала в виде параболоида вращения, усеченного параболоида,
параболического цилиндра или цилиндра специального профиля. Облучатель
помещается в фокусе параболоида или вдоль фокальной линии цилиндрического
зеркала. Соответственно для параболоида облучатель должен быть точечным, для
цилиндра – линейным. Наряду с однозеркальными антеннами применяются и
двухзеркальные.
Рассмотрим
принцип действия зеркальной антенны. Электромагнитная волна, излученная облучателем,
достигнув проводящей поверхности зеркала, возбуждает на ней токи, которые
создают вторичное поле, обычно называемое полем отраженной волны. Для того
чтобы на зеркало попадала основная часть излученной электромагнитной энергии,
облучатель должен излучать только в одну полусферу в направлении зеркала и не
излучать в другую полусферу. Такие излучатели называют однонаправленными.
В
раскрыве антенны отраженная волна обычно имеет плоский фронт для получения
острой диаграммы направленности либо фронт, обеспечивающий получение диаграммы
специальной формы. На больших (по сравнению с длиной волны и диаметром зеркала)
расстояниях от антенны эта волна в соответствии с законами излучения становится
сферической. Комплексная амплитуда напряженности электрического поля этой волны
описывается выражением
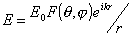 , ,
где
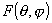 - нормированная
диаграмма направленности, сформированная зеркалом. - нормированная
диаграмма направленности, сформированная зеркалом.
Принцип
действия простейшей зеркальной антенны приведен на рисунке:
1
– зеркало, 2 – облучатель, 3 – сферический фронт волны облучателя, 4 – плоский
фронт волны облучателя, 5 – диаграмма направленности облучателя, 6 – диаграмма
направленности зеркала.
Точечный
облучатель (например, маленький рупор), расположенный в фокусе параболоида,
создает у поверхности зеркала сферическую волну. Зеркало преобразует ее в
плоскую, т.е. расходящийся пучок лучей преобразуется в параллельный, чем и достигается
формирование острой диаграммы направленности.
Геометрические
характеристики параболоидного зеркала.
Вспомним
основные геометрические свойства параболоида.
Нормаль
к поверхности параболоида в любой точке 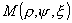 лежит в плоскости, содержащий
ось Z, и составляет угол лежит в плоскости, содержащий
ось Z, и составляет угол 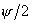 с прямой, соединяющей
эту точку с фокусом. с прямой, соединяющей
эту точку с фокусом.
Любое
сечение параболоида плоскостью, содержащее ось Z, является параболой с фокусом
в точке F. Кривая, получающаяся при сечения параболоида плоскостью,
параллельной оси Z, является также и параболой с тем же фокусным расстоянием f.
Из
первого свойства следует, что если поместить точечный источник электромагнитных
волн в фокусе параболоида, то все лучи после
отражение будут параллельны оси Z.
Это
означает, что отраженная волна будет плоской с фронтом, перпендикулярным оси Z
параболоида.
Из
второго свойства следует, что для анализа вопросов отражения волн от
поверхности зеркала и наведения на нем токов можно ограничиться рассмотрением
любого сечения зеркала плоскостью, проходящей через ось Z или параллельно ей.
Кроме того, из второго свойства вытекает, что для контроля точности изготовления
параболического зеркала достаточно иметь только один шаблон.
При
анализе параболических зеркал удобно одновременно использовать различные
системы координат, переходя в процессе анализа от одной к другой, более удобной
для последующих расчетов. Такими системами координат являются:
Прямоугольная
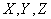 с началом в вершине
параболоида и осью Z, совпадающей с осью его вращения. Уравнение поверхности
зеркала в этой системе координат имеет вид с началом в вершине
параболоида и осью Z, совпадающей с осью его вращения. Уравнение поверхности
зеркала в этой системе координат имеет вид
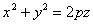 . .
Цилиндрическая
система 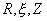 . Здесь . Здесь 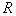 и и 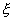 - полярные
координаты, отсчитываемые в плоскости Z=const. Угол - полярные
координаты, отсчитываемые в плоскости Z=const. Угол 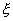 отсчитывается от
плоскости XOZ. Уравнение параболоида в этих координатах будет отсчитывается от
плоскости XOZ. Уравнение параболоида в этих координатах будет
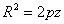 . .
Цилиндрическую
систему координат удобно использовать при определении координат точек истока
(т.е. точек источников поля).
Сферическая
система координат 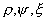 с началом в фокусе F
и полярной осью, совпадающей с осью Z. Здесь с началом в фокусе F
и полярной осью, совпадающей с осью Z. Здесь 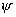 - полярный угол,
отсчитываемый от отрицательного направления оси - полярный угол,
отсчитываемый от отрицательного направления оси 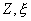 - азимут, тот же, что
в цилиндрической системе. Уравнение поверхности зеркала в этой системе
координат нами уже было получено: - азимут, тот же, что
в цилиндрической системе. Уравнение поверхности зеркала в этой системе
координат нами уже было получено: 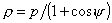 . Эта система координат удобна для описания диаграммы
направленности облучателя. . Эта система координат удобна для описания диаграммы
направленности облучателя.
Сферическая
система координат 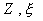 с началом в фокусе
параболоида. Здесь с началом в фокусе
параболоида. Здесь 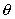 - полярный угол, отсчитываемый
от положительного направления оси Z; - полярный угол, отсчитываемый
от положительного направления оси Z; 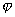 - азимут, отсчитываемый от плоскости XOZ. Эта система
координат удобна для определения координат точки наблюдения и будет
использована при расчете поля излучения. - азимут, отсчитываемый от плоскости XOZ. Эта система
координат удобна для определения координат точки наблюдения и будет
использована при расчете поля излучения.
Поверхность,
ограниченная кромкой параболоида и плоскостью 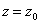 , называется раскрывом зеркала. Радиус , называется раскрывом зеркала. Радиус 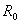 этой поверхности
называется радиусом раскрыва. Угол этой поверхности
называется радиусом раскрыва. Угол 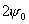 , под которым видно зеркало из фокуса, называется углом
раскрыва зеркала. , под которым видно зеркало из фокуса, называется углом
раскрыва зеркала.
Форму
зеркала удобно характеризовать либо отношением радиуса раскрыва к двойному
расстоянию (параметру параболоида) 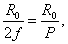 либо величиной
половины раскрыва либо величиной
половины раскрыва 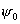 . Зеркало называют мелким,
или длиннофокусным, если . Зеркало называют мелким,
или длиннофокусным, если 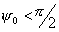 , глубоким, или короткофокусным, если , глубоким, или короткофокусным, если 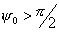 . .
Легко
найти связь между отношением 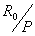 и углом и углом 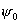 . .
Из
рис.1 следует, что
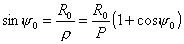 ; ;
откуда
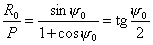 . .
У
длиннофокусного параболоида 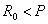 , у короткофокусного , у короткофокусного 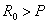 . При . При 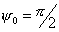 (фокус лежит в плоскости
раскрыва зеркала) (фокус лежит в плоскости
раскрыва зеркала) 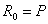 . .
Апертурный метод расчет поля
излучения.
В
апертурном поле излучения зеркальной антенны находится по известному полю в ее
раскрыве. В этом методе, в качестве излучающей рассматривается плоская
поверхность раскрыва параболоида с синфазным полем и известным законом
распределения его амплитуды.
Амплитудный
метод в том виде, в котором он используется на практике, является менее точным,
чем метод расчета через плотность тока. Это объясняется тем, что в этом случае
поле в раскрыве зеркала находится по законам геометрической оптики.
Следовательно, не учитывается векторный характер поля и, как результат этого,
не учитывается составляющие с паразитной поляризацией. Однако в пределах главного
лепестка и первых боковых лепестков, т.е. в наиболее важной для нас области
диаграммы направленности, оба метода практически дают одинаковые результаты.
Поэтому на практике наибольшее распространение получил апертурный метод расчета
как более простой.
Задача
нахождения поля излучения зеркальной антенны при апертурном методе расчета, как
и в общей теории антенн разбивается на две:
Вначале
находится поле в раскрыве антенны (внутренняя задача).
По
известному полю в раскрыве определяется поле излучения (внешняя задача).
А).
Определение поля в раскрыве параболоидного зеркала.
Поле
в раскрыве определяется методом геометрической оптики. Всегда выполняется
условие 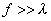 , следовательно, зеркало в дальней зоне и падающую от
облучателя волну на участке от фокуса до поверхности зеркала можно считать
сферической. , следовательно, зеркало в дальней зоне и падающую от
облучателя волну на участке от фокуса до поверхности зеркала можно считать
сферической.
В
сферической волне амплитуда поля изменяется обратно пропорционально 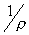 . После отражения от поверхности зеркала волна становится
плоской и амплитуда ее до раскрыва зеркала с расстоянием не изменяется. Таким
образом, если нам известна нормированная диаграмма направленности облучателя . После отражения от поверхности зеркала волна становится
плоской и амплитуда ее до раскрыва зеркала с расстоянием не изменяется. Таким
образом, если нам известна нормированная диаграмма направленности облучателя 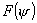 , поле в раскрыве зеркала легко находится. , поле в раскрыве зеркала легко находится.
Для
удобства расчетов введем нормированную координату точки в раскрыве зеркала
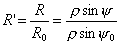 ; ;
Подставим
значение 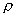 и и 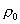
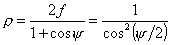
в
выражение для 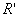 , после элементарных преобразований получаем , после элементарных преобразований получаем
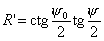 . .
Очевидно,
что 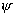 и и 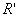 меняется в пределах меняется в пределах 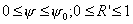 . .
Нормированное
значение амплитуды поля в раскрыве определится выражением 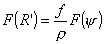 . .
Подставим
в последнюю формулу значение 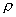 , получим окончательно , получим окончательно 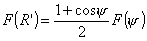 . .
Полученная
формула является расчетной. Из нее видно, что амплитуда поля в раскрыве зеркала
зависит только от радиальной координаты 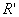 . Такая осевая симметрия в распределении поля явилась
следствием допущения, что диаграмма направленности облучателя является функцией
только полярного угла . Такая осевая симметрия в распределении поля явилась
следствием допущения, что диаграмма направленности облучателя является функцией
только полярного угла 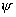 и не зависит от азимутального угла и не зависит от азимутального угла 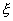 , хотя эта зависимость обычно выражена слабо. Вследствие
этого в большинстве случаев можно ограничиться расчетом распределения поля в
раскрыве только вдоль двух главных взаимно перпендикулярных направлений:
параллельного оси X и оси Y. Система координат X,Y,Z ориентируется так, чтобы
эти направления лежали в плоскости вектора , хотя эта зависимость обычно выражена слабо. Вследствие
этого в большинстве случаев можно ограничиться расчетом распределения поля в
раскрыве только вдоль двух главных взаимно перпендикулярных направлений:
параллельного оси X и оси Y. Система координат X,Y,Z ориентируется так, чтобы
эти направления лежали в плоскости вектора 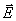 (плоскость XOZ) и вектора (плоскость XOZ) и вектора 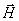 (плоскость YOZ). Для этих плоскостей затем и рассчитывается
поле излучения и диаграмма направленности антенны. Расчет ведется в
предположении, что поле в раскрыве зависит только от радиальной координаты (плоскость YOZ). Для этих плоскостей затем и рассчитывается
поле излучения и диаграмма направленности антенны. Расчет ведется в
предположении, что поле в раскрыве зависит только от радиальной координаты 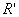 , а диаграмма направленности облучателя при расчете в
плоскости вектора , а диаграмма направленности облучателя при расчете в
плоскости вектора 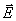 есть есть 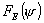 , а при расчете в плоскости вектора есть , а при расчете в плоскости вектора есть 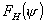 . .
Таким
образом, распределение поля в плоскости вектора 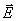 будет несколько отличаться от распределения в плоскости будет несколько отличаться от распределения в плоскости 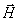 , что противоречит принятой зависимости распределения поля
только от радиальной координаты. Однако вследствие небольшого различия между
функциями , что противоречит принятой зависимости распределения поля
только от радиальной координаты. Однако вследствие небольшого различия между
функциями 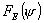 и и 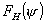 принятые допущения не
приводят к существенным погрешностям в расчетах и в тоже время позволяют учесть
различия в диаграмме направленности облучателя в плоскостях принятые допущения не
приводят к существенным погрешностям в расчетах и в тоже время позволяют учесть
различия в диаграмме направленности облучателя в плоскостях 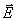 и и 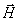 . .
Из
рис. видно, что наиболее интенсивно облучается центр зеркала, а поле к его
краям по амплитуде падает вследствие уменьшения значения 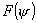 и увеличения и увеличения 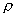 с увеличением с увеличением 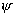 . Типичное распределение нормированной амплитуды поля в
раскрыве параболоидного зеркала показано на рис.: . Типичное распределение нормированной амплитуды поля в
раскрыве параболоидного зеркала показано на рис.:
Для
упрощения последующих расчетов найденное значение целесообразно аппроксимировать
интерполяционным полиномом
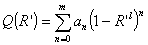 . .
Этот
полином хорошо аппроксимирует фактическое распределение поля в раскрыве
параболоида и для нахождения поля излучения при такой аппроксимации не
потребуется громоздких вычислений. Излучение круглой площадки с распределением
поля на ее поверхности, определяемым, уже было рассмотрено выше.
Узлами
интерполяции, т.е. точками, где полином 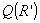 совпадает с ранее
найденной функцией совпадает с ранее
найденной функцией 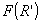 , будем считать точки раскрыва зеркала, соответствующие
значениям , будем считать точки раскрыва зеркала, соответствующие
значениям 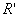 : : 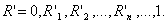 Тогда коэффициенты
полинома определяется из системы уравнений: Тогда коэффициенты
полинома определяется из системы уравнений:
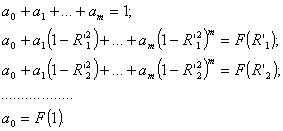
На
этом решение задачи определения поля в раскрыве параболоида можно считать
законченным.
При
инженерных расчетах для упрощения вычислений обычно можно ограничиться тремя
членами полинома, т.е. положить m=2. Тогда
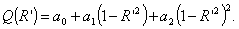
В
этом случае в качестве узлов интерполяции берут точки в центре раскрыва зеркала
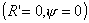 , на краю зеркала , на краю зеркала 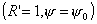 и приблизительно в
середине между этими крайними точками и приблизительно в
середине между этими крайними точками 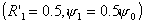 . Коэффициенты этого полинома определяются системой
уравнений: . Коэффициенты этого полинома определяются системой
уравнений:
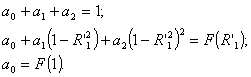
Относительная
погрешность, определяющая отклонение полинома от заданной функции 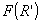 , может быть вычислена по формуле , может быть вычислена по формуле
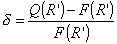 . .
Расчеты
показывают, что во многих случаях уже при трех членах полинома относительная
погрешность не превышает 1-2%. Если
требуется большая точность, следует брать большее число членов полинома.
Б).
Определение поля излучения параболоидного зеркала.
Раскрыв
зеркала представляет собой плоскую круглую площадку. Поле на площадке имеет
линейную поляризацию. Фаза поля в пределах площадки неизменна, а распределение
амплитуды описывается полиномом 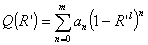 . .
Как
было показано выше, каждый n-й компонент
поля в раскрыве, представляемого полиномом, создает в дальней зоне напряженность
электрического поля 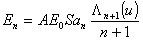 , где , где 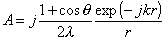 , S – площадь
раскрыва, E0 – амплитуда
напряженности электрического поля в центре площадки, , S – площадь
раскрыва, E0 – амплитуда
напряженности электрического поля в центре площадки, 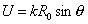 , , 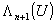 - ламбда-функция (n+1)-го порядка. - ламбда-функция (n+1)-го порядка.
Полное
поле в дальней зоне будет равно сумме полей, создаваемых каждым компонентом 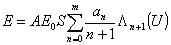 . .
Выражение,
определяемое суммой в последней формуле, представляет собой ненормированную
диаграмму направленности антенны:
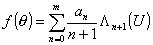
Для
получения нормированной диаграммы направленности найдем максимальное значение 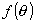 . Максимум излучения синфазной площадки имеет место в
направленности, перпендикулярном этой площадке, т.е. при . Максимум излучения синфазной площадки имеет место в
направленности, перпендикулярном этой площадке, т.е. при 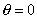 . Этому значению . Этому значению 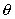 соответствует
значение соответствует
значение 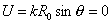 . Заметим, что . Заметим, что 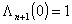 при любых n. Следовательно, при любых n. Следовательно, 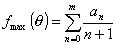 . .
Тогда
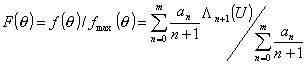
Эта
формула описывает нормированную диаграмму направленности параболоидной
зеркальной антенны и является расчетной. Постоянные коэффициенты 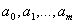 зависят от
распределения поля в раскрыве зеркала. Их значения определяются системой
уравнений зависят от
распределения поля в раскрыве зеркала. Их значения определяются системой
уравнений
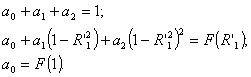
Если
ограничится тремя членами полинома, т.е. положить m=2, нормированная диаграмма направленности параболоидного зеркала
опишется выражением 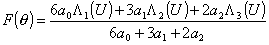 . .
Коэффициент
направленного действия и
коэффициент
усиления.
Коэффициент
направленного действия параболической антенны удобно определить через эффективную
поверхность 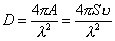 , где , где 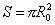 - геометрическая
площадь раскрыва, - геометрическая
площадь раскрыва, 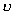 - коэффициент использования
поверхности раскрыва. - коэффициент использования
поверхности раскрыва.
Коэффициент
использования площади раскрыва зеркала полностью определяется характером распределения
поля в раскрыве. Как известно, для любых площадок, возбуждаемых синфазно, его
величина определяется формулой 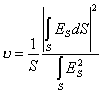 . .
В
случае параболоидного зеркала имеем
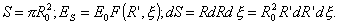
Тогда,
подставив значения, получим
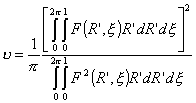 . .
Для
приближенного расчета 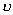 можно пренебречь
зависимостью распределения поля от можно пренебречь
зависимостью распределения поля от 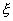 и считать, как мы это
делаем в апертурном методе расчета, что амплитуда поля в раскрыве является
функцией только координаты и считать, как мы это
делаем в апертурном методе расчета, что амплитуда поля в раскрыве является
функцией только координаты 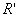 : : 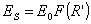 . В этом случае формула упрощается и принимает вид . В этом случае формула упрощается и принимает вид
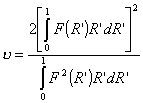 . .
Данная
формула в большинстве случаев дает вполне удовлетворительную точность и может
быть принята за расчетную.
В
качестве примера рассчитываем для двух случаев:
Амплитуда
поля в раскрыве неизменна 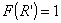 ; ;
Амплитуда
поля изменяется по закону 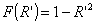 , т.е. на краях зеркала поле равно нулю. , т.е. на краях зеркала поле равно нулю.
Расчет
по формуле дает для первого случая 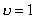 и для второго и для второго 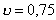 . .
В
реальных антеннах величина зависит от
типа облучателя и формы (т.е. глубины) зеркала.
На
рисунке показана зависимость коэффициента использования поверхности раскрыва 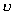 от угла раскрыва от угла раскрыва 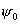 для случая, когда
облучателем является диполь с дисковым рефлектором. Распределение поля в
раскрыве зеркала, облучаемого таким облучателем, является типичным для многих
практических случаев. для случая, когда
облучателем является диполь с дисковым рефлектором. Распределение поля в
раскрыве зеркала, облучаемого таким облучателем, является типичным для многих
практических случаев.
Из
приведенного рисунка видно, что коэффициента 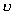 достигает единицы,
когда достигает единицы,
когда 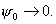 Это объясняется тем,
что поле в раскрыве очень мелких зеркал близко к равномерному. С увеличение
глубины зеркала коэффициент Это объясняется тем,
что поле в раскрыве очень мелких зеркал близко к равномерному. С увеличение
глубины зеркала коэффициент 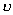 довольно быстро
падает. довольно быстро
падает.
Коэффициент
направленного действия, определяемый как
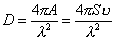 , ,
не
учитывает потерь энергии на рассеивание, т.е. потерь энергии, проходящей от
облучателя мимо зеркала.
Поэтому
КНД параболических зеркал в отличие от рупорных антенн не является параметром,
достаточно полно характеризующим выигрыш, получаемый от применения направленной
антенны. Для более полной характеристики следует использовать такой параметр,
как коэффициент усиления антенны
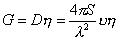 , ,
где
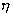 - коэффициент
полезного действия. - коэффициент
полезного действия.
Тепловым
потерям электромагнитной энергии на поверхности зеркала можно пренебречь. Тогда
под К.П.Д. параболической антенны следует понимать отношение мощности, падающей
на поверхность зеркала 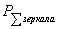 , к полной мощности излучения облучателя , к полной мощности излучения облучателя 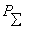 : :
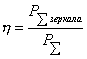
Для
определения этого отношения окружим облучатель сферой радиусом 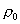 .Элемент поверхности сферы равен .Элемент поверхности сферы равен 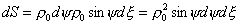 . Полная мощность излучения облучателя определяется выражением . Полная мощность излучения облучателя определяется выражением
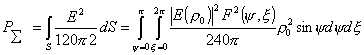 , ,
где
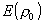 - амплитуда
напряженности поля в направлении максимального излучения облучателя; - амплитуда
напряженности поля в направлении максимального излучения облучателя; 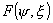 - нормированная
диаграмма направленности облучателя. - нормированная
диаграмма направленности облучателя.
Соответственно
мощность излучения, попадающего на зеркала будет
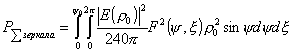 . .
Таким
образом, коэффициент полезного действия параболической антенны равен 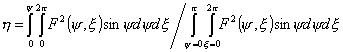 . Из этого выражения видно, что К.П.Д. целиком определяется
диаграммой направленности облучателя и величиной . Из этого выражения видно, что К.П.Д. целиком определяется
диаграммой направленности облучателя и величиной 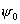 . .
Очевидно,
чем больше угол 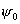 , т.е. чем глубже зеркало, тем большая часть излученной
энергии попадает на зеркало и, следовательно, тем больше К.П.Д.. Таким образом,
характер изменения функции , т.е. чем глубже зеркало, тем большая часть излученной
энергии попадает на зеркало и, следовательно, тем больше К.П.Д.. Таким образом,
характер изменения функции 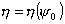 противоположен
характеру изменения функции противоположен
характеру изменения функции 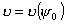 . .
Вычислим
К.П.Д. для случая, когда облучателем является диполь с дисковым рефлектором.
Диаграмма такого облучателя может быть выражена следующим образом
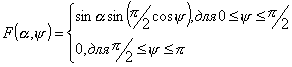 . .
Для
дальнейших вычислений необходимо выразить угол 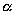 через углы через углы 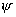 и и 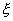 . Для этого рассмотрим рисунок, на котором плоскость . Для этого рассмотрим рисунок, на котором плоскость 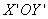 параллельна плоскости
раскрыва и проходит через точку параллельна плоскости
раскрыва и проходит через точку 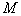 на его поверхности, а
ось на его поверхности, а
ось 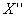 совпадает с осью
диполя и параллельна оси совпадает с осью
диполя и параллельна оси 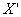 . Из рисунка видно, что . Из рисунка видно, что
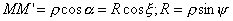 . .
Отсюда
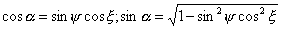 . .
Таким
образом
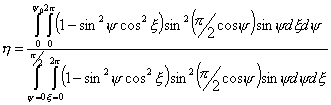 . .
В
последней формуле интегрирование по 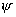 производится от 0 до производится от 0 до 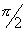 , так как мы считаем, что облучатель излучает только в
переднюю полусферу. , так как мы считаем, что облучатель излучает только в
переднюю полусферу.
Интегрирование
в этом случае упростится, а результат изменится незначительно, если положить 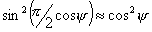 . .
В
этом случае интеграл легко берется и КПД оказывается равным
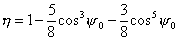 . .
Полученная
формула дает простую зависимость КПД параболической антенны от угла раскрыва 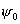 зеркала для случая,
когда облучатель является электрическим диполем с дисковым рефлектором.
Вследствие этого последняя формула может быть использована для ориентировочной
оценки КПД параболоидных антенн во многих практических случаях. зеркала для случая,
когда облучатель является электрическим диполем с дисковым рефлектором.
Вследствие этого последняя формула может быть использована для ориентировочной
оценки КПД параболоидных антенн во многих практических случаях.
Коэффициент
усиления 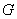 зеркальной антенны
согласно пропорционален произведению зеркальной антенны
согласно пропорционален произведению 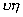 . Вследствие разного характера зависимости сомножителей от . Вследствие разного характера зависимости сомножителей от 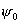 это произведение
должно иметь максимум. это произведение
должно иметь максимум.
В
некоторых случаях под термином коэффициент использования поверхности (КИП)
понимается величина 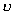 , а произведение , а произведение 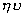 . В реальных параболических антеннах значение . В реальных параболических антеннах значение 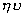 имеет величину имеет величину 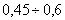 . .
|